Dive 95: There’s always another way…
Hey, it’s Alvin!
One of the biggest complaints about the North American education system is the state of math education. But no one seems to know how to fix it. Hey, I get it. Because I was a student of the Canadian education system, which is similar enough to the American one that we complain about math education too.
There are 2 glaring problems:
We obsessively fixate on the most popular solution to a problem when other solutions exist that may be better.
We’re just not learning enough from the best.
When we see someone who’s exceptional at math, we treat them as exceptions to the rule. That’s why we call them “math geniuses.” Then, the rest of us resign ourselves to the idea that “math is hard.” And that’s where we stop. But why?
Maybe it’s true that some people’s brains are more “wired” for math. But that doesn’t mean there’s nothing the rest of us can learn from them to improve our own math skills.
Yes, I had plenty of classmates who thought math was hard. But I also knew a handful who thought math was easy. And the latter often shared one common opinion about the math we were taught in school:
The methods we were taught were “dumb.”
“Dumb” means we’re often taught inefficient algorithms. An algorithm being a set of problem-solving processes and rules. These inefficient algorithms fool us into believing that math is hard, which hampers our ability to tackle more advanced math. When, in fact, we’re just using the wrong tool for the job. It’ll be easier for us to understand why with an example.
So, I pulled this simple example from the late Professor Alexander Bogomolny’s Cut-the-Knot math website. Consider this question:
A quantity and its 1/2 added together become 16. What is the quantity?
Most people who studied algebra could recognize this as an algebra problem. You’d start by declaring the unknown quantity with a letter variable like, ‘x’. Then, you’d restate the problem as a math equation, like:
Then, you’d solve for ‘x’.
If you spent most of your formative years in the North American education system, then you were taught a specific algorithm for solving this problem with minor variations here and there. For example, you’d start by reducing the variable ‘x’ so there’s only one of them. Then you’d perform operations on both sides of the equal sign so only the ‘x’ remains on one side, and a single number (the answer) remains on the other. Something like:
If you were proficient enough, you could skip a step or two. But we were taught that this is THE way to solve this kind of problem. Generally, we were not taught alternatives. But…
There is always more than one way to solve a problem.
What if I told you there is a simpler approach?
What if I told you the simpler approach takes just TWO steps?
In fact, what if I told you that you don’t even need to represent the unknown as a letter to solve this algebra problem?
Here, again, is the original problem:
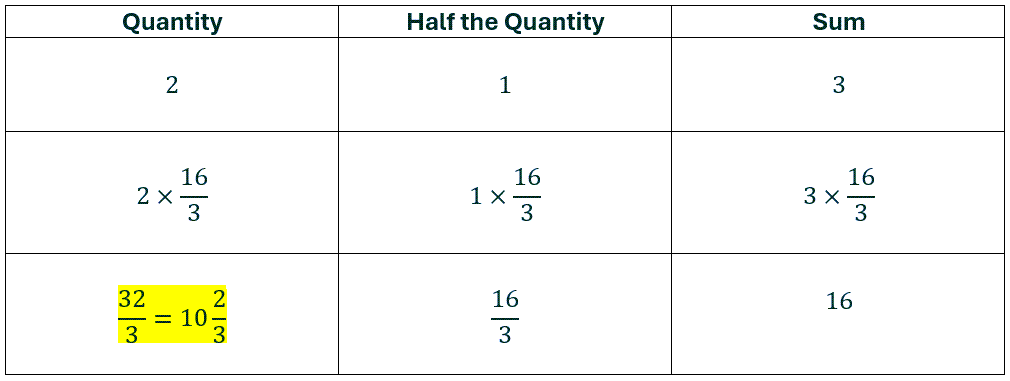
A quantity and its 1/2 added together become 16. What is the quantity?
Let’s just assume the quantity is: 2.
The quantity (2) and its ½ (1) added together become 3. So, that’s wrong because we want 16. Not 3. But we can get a result of 16 if we then multiply 3 by 16/3. And since we’re multiplying the result, we also need to multiply the other values by the same amount. So, here’s the full approach:
I’m not saying that the second approach is always better or that it will always work. But it’s much simpler, at least, for this problem. The point is:
There is always more than one way to solve a problem.
And if you want to get better at math, it helps to simplify your approach to problem-solving at every level. Because as you advance, the equations get more complex in more than one way. There’s already so much you need to think about and track with the 6-step algorithm. It’s easy to see why many people feel overwhelmed when they see brackets, exponentials and imaginary numbers thrown into the mix. It’s easy to see why math seems hard.
The first approach just doesn’t scale up well. There’s nothing mathematically wrong with it. It gives the right answer. But while it’s fine for learning number theories, it takes too much effort in practice. So, solving problems this way becomes a struggle. And students get stuck at a specific competence level.
When we understand the underlying theory of an approach, we achieve what psychologists call “conscious competence.” In fact, there are 4 stages of competence:
Unconscious incompetence (when a person sucks and doesn’t know they suck)
Conscious incompetence (when a person sucks and knows they suck)
Conscious competence (when a person rocks, but it takes a lot of mental effort)
Unconscious competence (when a person rocks and it takes little to no effort)
Those who believe “math is hard” are stuck on stage 3. In fact, this is true for whatever new skill you pick up. Recognize when you’re feeling like, “I know how to do well, but this is really hard.” Because it’s a sign that you’re likely consciously competent. And it’s easy to get stuck there if you’re passive about improving your skill level. But there’s a way up…
This is when you need to take some initiative. Look for experts who make the skill look super easy. Connect with them to see if they’ll share their views. Someone who looks like a “math genius” probably looks at math differently from you. They probably have a way of simplifying the problem that you don’t know about. In fact, they probably know shortcuts that will help you flip the frame on the problem.
If there’s one thing I wish schools did a better job of teaching, it’s:
There is always more than one way to solve a problem.
In a modern society so obsessed with diverse thinking, it’s surprising how often we still confine ourselves to a single (often complicated) solution to complex, open-ended problems. I’m not just talking about math problems. Even popular social problems have multiple solutions. Why limit ourselves to the one that politicians, celebrities and influencers force on us?
Instead of seeing what they want you to see, you got to open your brain to the possibilities.
- King Bumi from Avatar: The Last Airbender
Reply to belowthesurfacetop@gmail.com or click “Message Alvin” below if you have questions or comments. I’d love the hear from you.
Thank you for reading. Look for simpler solutions. And I’ll see you in the next one.



Great article! I always thought the intuitive, commonsense approach you suggested was “cheating”. In fact my math teachers made us show our calculations to confirm we’d gotten the answer the “right” way—only then was the answer “right”.